Search the Community

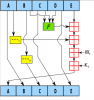
Introduction: I'm in the process of teaching myself how our modern computer cryptographic functions work, and also (eventually) making my own. I started looking into cryptography last July, and have been working on it on and off since then. This thread will consist of my attempts at both recreating the current standards visually in Excel, and developing my own methods. Doing this more as a proof of concept because I am not a computer programmer by trade and such do not know how to make a truly applicable algorithm. If at some point I get extremely daring, I'll try to bring it out of excel and into an actual application. Feedback and input is always welcomed. I can also get into the finer details of the actual Excel formula-side if requested. If unspecified I will simply give the executive summary at every relevant checkpoint. To start the thread it will be a bit of a catch up and a learning curve, but in the followup posts I will try to more fully explain the process/terms. Apologies if I made some mistakes in the very brief description of the algorithms and my recreations. These were completed over six months ago and I'm a little fuzzy on much of the underlying specifics that were being dealt with at the time. Again, as a disclaimer I am not well-versed in computer programming, especially at the bit by bit level, let alone the upper-level language-level. Everything expressed here is to the best of my understanding at the time of posting. As such, if I make a mistake in defining terminology, a concept, etc please correct me otherwise I'm just throwing stuff at a wall and hoping it sticks. Thank you, Songbirdo Recreation in Excel: The recreation starts with the white paper taken from the NIST.gov website: http://csrc.nist.gov/groups/ST/toolkit/examples.html The white papers provide the pseudo-code as well as the function outputs so I may check my work for accuracy. After deciphering the pseudo-code (and looking up a lot of terms on Wikipedia that I don't understand), I attempt to recreate it in Excel. This process has its difficulties as Excel cannot be iterative (a cell cannot reference and write to itself) so additional cells and lines are required for the multiple cycles that these algorithms use. Excel is also very picky with what a 1 (as a number) and 1 (as a piece of text) is. The workaround is simply to use an If/then function to specify the text as a number, and vice versa where needed. Excel also does not have an XOR function (at least my version), and nesting the necessary AND OR functions proved fruitless. So I did a tabular addition and manually carrying the remainders to do the MOD32 additions. For the bit-wise XOR function I just did a simple if/then scenario (where if one is 1 and the other is 1, it will output 0, etc). I tried to colorize by word (the primary color) and then the different shades of that color to help distinguish between each hexadecimal (four bit) sections. (Necessary to keep track of later during the Rubik's twists, see below). The colorization also helped keep track of where each string of the bits were originating from (especially for bit rotations, see SHA-512 spreadsheet and the Wt formulation table - teal blue with speckles of orange red and yellow). SHA-1 (Secure Hash Algorithm): I started with the asymmetric compression function: SHA-1 http://en.wikipedia.org/wiki/SHA-1 It is basically a password encryption function. One-way, "cannot" be reversed. Pictorially it looks something like this: ABCDE are five separate "words" of 32 bits (1's and 0's) each in length. The <<<< are bit rotations, F is a function, the box with a cross through it are XOR (exclusive or) boolean algebra, Wt and Kt are words based on your password (input). After working out the translational problems with Excel I got a working model of the SHA-1 Preview: Link to the full spreadsheet:https://mega.co.nz/#!44U1lZAT!VdAt8f8F9f9Zxd7a8jqkPYDgelwNLD3Cx543II_K2bs Compare the hash values you obtain in the spreadsheet with: http://www.fileformat.info/tool/hash.htm?text=abc SHA-2 (Secure Hash Algorithm): The SHA-1 is no longer as widely used as it once was mainly because it isn't as secure as it used to be. So I moved onto the SHA-2 (specifically the SHA-512 for 512 bit encryption). http://en.wikipedia.org/wiki/SHA-2 The underlying algorithm looks pictorially like this: Muuuuch more complex. This is a 512 bit (8 - 32 bit words). Thankfully the white paper had step-by-step outputs so I could check my work. I made three or four minor mistakes that completely changed the outcome. Picture of one cycle comparison (each color is a different Word, Blue = A, Red = B, etc) Link to the full spreadsheet: https://mega.co.nz/#!09UBkR6D!WXl1-wohIAvaEl0RZD_vISlxgJ1NSKXr50K09U90eHQ AES (Advanced Encryption Standard): Onto what I'm working on now! The AES Block Cipher is fancy way of saying "encrypting information (think file encryption) that can be reversed with the password". http://en.wikipedia.org/wiki/Advanced_Encryption_Standard The AES appears to use a combination of 128 (10 cycles), 192 (12 cycles) and 256 (14 cycles) bit encryption and applying four functions per cycle. It encrypts based on an array of bits (2D representation of the bits) instead of a string (one dimensional representation of the bits) like the SHA-512 did. The fact this uses an array excites me as this means its proof that these encryption algorithms can be brought to three dimensions (and more!). And then all sorts of cool functions can be applied, I'll give you a hint: Anyway, need a working AES model before getting into the Rubik's rotations, but I've already got separate spreadsheets to assign and rotate bits in a similar fashion (or at least similar block sizes, may need to adjust them to the correct bit size of the block ciphers) The four functions of the AES are SubBytes (Byte substitution), ShiftRows (similar to a bit rotation, except for the whole row of bits), MixColumns (which I'm currently figuring out) and something called a Round Key value (unsure what this is for as of now, but I know it's based on your key/password). Screenshot of Current Progress (4/1/2014): SubBytes (COMPLETED): take a cell, and based on what the 8 bits are, substitute it with a different 8 bits (shown in hexadecimal format): Copied from the white paper. The colorization was done to error check my typing. I did make an error, enclosed in a box. The lower right one was 93, where it should have been 9e. The columns on the right are reformatting the original table so that the VLOOKUP excel function can be utilized. ShiftRows (COMPLETED): MixColumns (RESEARCHING): RoundKey (RESEARCHING): Reversible XOR (Exclusive Or): One of the really cool things I realized about the XOR function is that it's reversible by reapplying the imput. Which is why the Block Cipher works symmetrically to encrypt and decipher your files. That's the fundamental difference between this block cipher and the compression function SHA. For example, say your (key) is "1" If you (file) is 1 or 0 1 (key) XOR 1 (file) = 0 (output) 1 (key) XOR 0 (file) = 1 (output) So your encyrpted (file) is either 0 if your starting was 1, and 1 if your starting was 0. Apply the key again: 1 (key) XOR 0 (output) = 1 (file) 1 (key) XOR 1 (output) = 0 (file) Tada! Back where you started. The SHA uses a Mod 32 summation to combine separate words. Think of Mod summation like a 12 hour face-clock. It goes from 1 to 12, then goes back to 1, and keeps going around. Mod 32 is like a clock except for 32 bits (the number itself is actually 232 where a clock is just 12). This means when you reach 232, it ticks over and starts from 0 again. If you try to undo that, you don't know if it cycled once, twice, or even at all. This is part of the reason why the compression functions are nearly impossible to crack. This large summation happens 80 times in the SHA-512, consisting of about 10 rows of bits: The largest remainder I've seen (how many times the specific bit cycled between 1 and 0) is nine. So the 232 "clock" looped around up to nine times per cycle, at two positions in the algorithm,and again over 80 cycles, or a total possibility of looping up to 1440 times! Customizable Encryption Algorithms: I had the realization one day driving home that you need two things in order to break an encryption (excluding the obvious: computer, electricity, network, etc etc...). You need the key (password) AAAND you need the algorithm in which it was encrypted. Without both, you cannot possibly hope to decipher the encrypted file. Where the Rubik's Cube "twist" comes into play (once the AES is brought to the third dimension) is the ability to scramble a block or multiple blocks beyond recognition. The rotation algorithm in which you scramble it would be user-chosen and so the encryption algorithm itself becomes customizable. Even if you manage to steal a key (password) to access the files, without the Rubik's rotation algorithm as input, you don't have the appropriate algorithm to decipher it. It's like finding a key on the side of the road but not knowing which lock it was intended to open. Imagine a company having a personalized encryption algorithm proprietary to that company and their network. Talk about secure information storage! This reminds me of what the banks and other online companies use for authentication: two really big prime numbers multiplied together. They store the product openly, but without the two prime numbers to generate the product you cannot be authenticated.